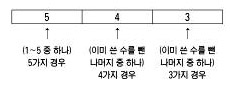확률을 알면 ‘현명한 선택’ 가능해요

수학개념 쏙쏙 /

빨래를 하려고 아빠의 양복 주머니를 살피던 엄마가 번호가 적힌 한 장의 메모를 꺼냈다. “아니, 여보, 요즘도 로또를 한단 말이에요?” 아빠는 머리를 긁적긁적하였다. “재미로 하는 거지 뭐….” 엄마, 아빠의 이야기를 듣고 있던 선일이가 아빠에게 물었다. “아빠, 로또가 뭐에요?” “그건 말이다. 1부터 45까지의 수 중에서 6개를 고르는 거야. 6개를 모두 맞추면 1등이란다.” “똑같은 수를 써도 되요?” “아니. 한 번 쓴 수는 또 쓸 수 없단다.” “그러면 만약에 제가 1, 2, 3, 4, 5, 6을 골랐잖아요. 그런데 당첨 번호가 6, 5, 4, 3, 2, 1이면 저는 떨어진 거에요?” “아니. 순서는 상관없단다. 그냥 6개의 수를 맞추면 되는 거야.” 듣고 있던 엄마는, “45개의 수 중에서 6개를 맞추는 게 쉬운 일이니? 낙타가 바늘구멍에 들어갈 일이지.”하였다. 거실 바닥에 있던 신문지에 한참 계산을 하던 선일이. “아빠, 6개의 수가 될 경우는 모두 814만5060가지에요. 그러니까 아빠가 고른 수가 당첨될 확률은 1/814만5060 이란 거죠.” “뭐라고? 네가 그걸 어떻게 계산했니?” “ 흐흐… 그건 비밀이에요! 암튼 당첨될 확률이 엄청 작으니까 안 하는 게 나을 것 같아요.” 아들의 말에 아빠는, “쩝, 확률이 작으니까 그만큼 당첨금이 높은 게 아니냐.” 하며 입맛을 다셨다.

선일이는 어떻게 계산했을까? 1부터 45까지의 수 중에서 6개의 수를 고르는 경우의 수는 어떻게 구하는 지 알아보기에 앞서, 좀 더 작은 수의 경우를 먼저 알아보자.

1부터 5까지의 수 중에서 3개의 수를 뽑는 방법은

과 같으므로 나열된 순서가 다른 경우까지 모두 세면

60가지이다.

5×4×3=60

하지만 이 때, 주의할 것이 있다. 우리는 1부터 5까지의 수 중에서 3개의 수를 ‘뽑는다’(순서대로 ‘나열한다’가 아니고 단지 뽑는다는 것)고 하였다는 것에 주목해야 한다. 나열한다고 할 때는 123은 132와 다르다. 하지만 뽑기만 할 때는 123과 132는 같은 경우이므로 순서가 달라도 종류가 같다면 한 가지로 보아야 한다. 위의 각 세로 줄에는 6가지 경우가 있지만 어쨌든 사용된 수는 모두 같다. 따라서 수의 종류만 따지자면 각 줄은 1가지로 보아야 한다. 그러므로 전체 경우의 수의 1/6이 우리가 구하고자 하는 경우의 수이다. 따라서 답은 60/6 = 10 (가지)이다.

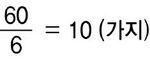즉, (1,2,3), (1,2,4), (1,2,5), (1,3,4), (1,3,5), (1,4,5), (2,3,4), (2,3,5), (2,4,5), (3,4,5)가 나온다.

처음으로 돌아와서, 1부터 45까지의 수 중에서 6개의 수를 고르는 경우에 대해 알아보자. 이 때도 먼저 고르던 나중에 고르던 수를 고르는 순서는 상관이 없다. 따라서 위와 마찬가지 방법으로 계산할 수 있다. 먼저, 6개의 수가 서로 다른 순서로 나열될 때의 경우의 수를 구한다.

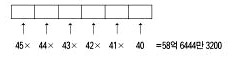이 때, 똑같은 6개의 수가 순서만 다르게 나열하는 가짓수는 720(6×5×4×3×2×1=720)가지이다. (123456=123465=...=654321) 순서가 달라도 고른 6개의 수가 같다면 결국 720가지가 아니라 1가지로 보아야 한다. 따라서 전체 가짓수인 58억 6444만 3200을 720으로 나누어야 한다.

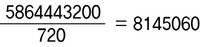따라서 45개의 수에서 순서에 상관없이 6개를 고르는 방법의 수는 모두 8145060이다. 그 중 하나의 수가 1등 당첨번호이므로, 당첨될 확률은 1/8,145,060이다. 이것이 선일이가 구한 방법이다.

그나저나 경우의 수나 확률은 왜 배우는 걸까? 학생들은 아직 어리기 때문에 생활 속에서 경우의 수와 확률을 알아내서 판단해야만 하는 일은 별로 없다. 하지만 어른이 되어 사회생활을 하게 되면 여러 가지 경우 중에서 어떤 경우를 선택하는 것이 가장 좋을까를 알아보아야 할 일이 많아지게 된다.

예를 들어 축구를 좋아하는 아이가 자라 대표팀 감독이 될 수도 있다. 감독은 우리나라 축구 선수들 중에 어떤 선수를 대표팀에 넣을지, 대표팀에 선발된 선수들의 포지션을 정할 때도 여러 가지 경우를 생각해야 한다. 열혈 축구 팬이 되었다면 각 팀의 우승 확률을 계산하여 우리가 어떤 조에 들어가는 것이 가장 유리한지를 따져 볼 수도 있다. 또 지금 당장 진학할 학교를 선택할 때도 우리는, 우리 동네의 여러 중학교 중에서 어떤 학교를 선택할까, 그리고 여러 고등학교 중에서 어떤 학교에 지원할까를 고민한다.

이것과 같이 우리는 늘 “어떤 경우가 가장 좋을까?”하는 판단을 해야 하고 그에 관련된 계획을 세우게 된다. 종이와 연필을 써서 표를 그리진 않지만, 우리는 우리도 모르게 여러 가지 경우의 수에 대해 따지고 있는 것이다. 이 모든 것에는 경우의 수와 확률 이론이 들어 있다. 만약 경우의 수와 확률을 배우지 못한다면 어떻게 될까? 아마도 모든 것을 그저 운명에 맡겨야 할 것이다. 이런 의미에서 본다면, 학교 교육 과정에서 경우의 수와 확률을 배우는 이유는 바로 ‘선택의 순간에 좀 더 현명한 판단을 하기 위해서’이다.

강미선/수학 칼럼니스트 [e-mail]