등록 : 2006.06.18 19:58
수정 : 2006.06.21 18:34
논리로 배우는 수학
“그동안 민주노동당이 의회 진출 이후 제 역할을 못한다는 얘기를 많이 들었는데, 오늘은 큰 보람과 대단한 자부심을 느낍니다.” 박용진 민주노동당 대변인은 여야의 극한 대치 상황 속에서 ‘주민 소환제법’이 국회를 통과한 지난달 2일 이렇게 감회를 밝혔다. 지방자치단체의 비리와 부패를 단죄할 핵심 수단인 주민소환제법을 원내의석 9석의 초미니 민주노동당의 ‘캐스팅 보트’ 전략으로 통과시켰다는 만족감을 드러낸 것이다.
민주노동당은 그동안 지방자치단체장이나 지방의원들이 비리를 저질러도 유권자는 손쓸 방도가 없는 현행 지방자치제의 모순을 해소하려면 주민소환제를 도입해야 한다고 줄기차게 주장해왔지만, 한나라당의 반대와 열린우리당의 미온적 태도 때문에 좌절감을 맛봐야 했다.
그러나 열린우리당이 뒤늦게 찬성 태도를 밝히면서 희망이 보이기 시작했다. 김원기 국회의장이 직권상정 대상에서 주민소환제법안을 빼놓아 다시 무산될 뻔했으나 민노당이 열린우리당에 주민소환제법안 등을 본회의 참여의 조건으로 내걸면서 결국 입법에 성공했다.
20세기에서부터 투표는 총칼 없는 전쟁으로 불려왔다. 그것은 투표를 통해서 모든 의사결정이 이루어지기 때문이다. 이제는 지구촌은 무기를 들고 직접적인 전쟁을 하는 것은 일부 분쟁지역을 제외하고는 거의 볼 수가 없다. 그러나 시대가 흘러서 투표 상황은 우리 일상 주변에서 너무나 자주 일어나며 생활 깊숙이 자리잡고 있다. 위에 든 예와 같이 어떻게 해서 소수 정당인 민주노동당이 이번 임시국회에서 중요 민생 법안 통과의 결정적인 캐스팅보트를 행사하는 것이 가능할까?
이와 같은 상황은 언뜻 수학과는 관련 없는 듯하지만 이제는 버젓이 수학과의 내용으로 교과서안에 들어와 있다는 사실은 놀랄 일이 아니다. 우리나라는 이런 실제적인 수학이 학교에서 너무나 늦게 도입되었다. 7차 교육과정에서 수학과의 심화선택과목으로 도입된 이산수학 교과서에 의사결정과 최적화라는 단원에서 그 내용을 볼 수 있다. 늦게나마 이런 실제적인 내용이 수학에서 가르쳐진다는 것만으로도 학생들은 수학이 우리 생활과 전혀 무관한 것으로 생각하는 것이 잘못임을 깨닫게 할 수 있어 다행이다.
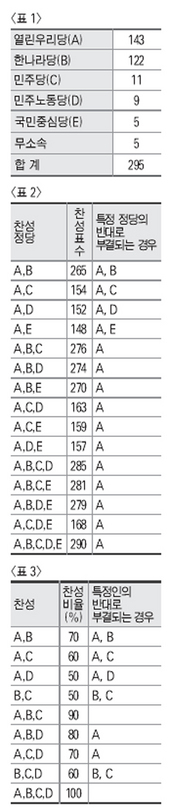
이제 이산수학 교과서에서 다루는 투표의 영향력에 대하여 알아보자. 현재 우리나라의 국회의원 정수는 299명이며, 이 중에서 지방선거 출마로 의원직 사퇴했거나 선거법위반과 정치자금법 위반으로 의원직 상실한 4명을 제외한 295명의 소속 정당별 인원수는
<표1>과 같다.
예를 들어 국회에서 어떤 안이 통과되려면 과반수 찬성표를 받아야 하고, 각 당의 국회의원은 당론을 정하여 투표한다고 치자. 그리고 지금은 무소속을 제외하고 생각하자. 우리가 궁금한 것은 투표에 대한 각 당의 영향력이 의석수에 비례하는지의 여부이다. 아니라는 것은 짐작했을 것이다. 그것은 앞에 설명한 5월2일의 임시국회 투표 결과를 보면 알 수 있다. 하지만 실제로 수학에서는 어떻게 계산을 할까? 다음에 예로 든 것은 투표에서의 영향력을 계산하는 한 가지 방법이라고 생각하면 된다.
(1) 우선 모든 국회의원이 투표를 할 때 그 결과로 과반수인 148을 넘는 경우를 나타내면 다음
<표2>와 같다.
(2) 찬성을 하면 안건이 통과되지만 특정 정당이 반대로 돌아설 경우 부결되는 경우를 나열하면 표에서 보는 바대로 19가지 경우가 가능하며 각 당이 나오는 횟수는 다음과 같으며, 이것을 근거로 영향력을 계산한다.
A : 15, B : 1, C : 1, D : 1, E : 1
(3) 이 때 각 당의 영향력은 다음과 같다.
어떤 결과가 나왔는가? 비록 열린우리당은 과반의석을 차지하고 있지는 않지만 투표에서의 영향력은 80%에 육박한다. 이것은 현 의석 분포로도 열린우리당은 큰 힘을 가지고 있다는 것을 알 수 있다. 어느 한 당하고만 연합해도 과반수를 넘길 수 있다. 반면 나머지 네 정당은 의석수는 많은 차이가 있지만 영향력은 모두 5% 정도로 똑같다. 신기하고 이상한 일이 아닐 수 없다. 이게 투표라는 ‘게임’의 현실이다. 그러니 의석이 10석도 안되는 민주노동당이 122석의 한나라당과 똑같은 영향력을 가지고 있으니 캐스팅보트를 쥐고 있다는 말이 거짓이 아님을 이해했을 것이다.
투표에서의 영향력은 오늘날 경제 사회의 대표격인 주식회사에서 흔하게 볼 수 있다. 주식회사는 주주총회에서 중요한 의사결정을 하게 되며, 주주총회에서의 투표수는 각 사람이 가지고 있는 지분 비율로 정한다. 예를 들어 A는 40%, B는 30%, C는 20%, D는 10%의 지분을 가지고 있다고 하자. 50% 이상의 찬성으로 어떤 안이 통과된다고 하면, 국회에서의 투표와 마찬가지로 다음과 같은
<표3>을 만들 수 있다.
찬성을 하면 안건이 통과되지만 특정인의 반대로 부결되는 경우는 12가지 경우가 가능하며 각 사람이 나오는 횟수는 다음과 같다.
A : 5, B : 3, C : 3, D : 1
그러므로 각 사람의 영향력은 다음과 같다.
이 경우를 보면 일단 각 사람의 지분의 비율과 투표의 영향력은 같지 않다는 것을 알 수 있다. 또 지분 비율이 10% 차이 나는 B와 C의 영향력이 똑같으며, D의 영향력은 지분 비율만도 못할 수도 있음을 알 수 있다. 따라서 투표에서의 영향력은 그 비율에 따라 교묘하게 달라짐을 이해한다면 오늘날 투표에서 이기는 비결은 바로 수학에 있음을 이제 깨달았을 것이다.
최수일/서울 용산고 교사
choisil@mathlove.org
광고

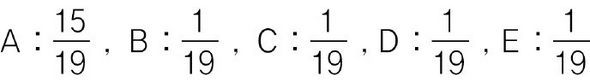
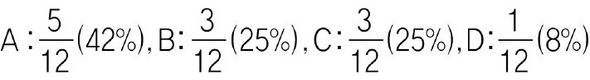


기사공유하기