등록 : 2006.06.25 20:01
수정 : 2006.06.26 15:53
수학개념 쏙쏙
지난번에 이어 수와 도형이 어떻게 연결되는지 좀 더 알아보도록 하자.
도형에서 가장 기본이 되는 것은 ‘점, 선, 면’이다. 그리고 계산에서는 덧셈, 뺄셈, 곱셈, 나눗셈이 기본이다. 먼저, 성냥개비 5개를 같은 방향으로 이어 놓자.
성냥개비에서 나무로 된 부분을 ‘선분’, 성냥개비의 머리를 ‘점’이라고 할 수 있다. 이 성냥개비를 <문제 푸는 방법 찾기> 단원에 자주 나오는 문제 중에, ‘도로에 나무 심기’ 문제와 연결해서 생각해 보자.
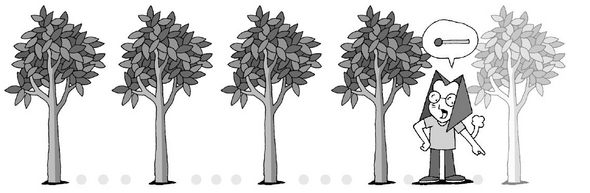
도로에 나무 심기 문제란, 예를 들면 “길이가 100미터인 도로에 5미터 간격으로 나무를 심으려 한다. 도로 양 끝에 반드시 나무를 심어야 한다면, 나무는 모두 몇 그루가 있어야 하겠는가?”하는 문제를 말한다.
여러분들 중에는 직접 그림을 그려본 후에야, 20에 1을 더 더했어야 했는데 미처 그 생각을 하지 못했다는 것을 나중에 깨달은 사람도 있을 것이다. 그런데 왜 이런 문제에서는 반드시 도로 양끝에 나무를 심어야 한다는 조건이 있는 걸까? 도형에서 ‘선분’은 양 끝이 막혀있어야 한다. 다시 말해서, 선분의 양끝은 ‘점’이다. 도로에 나무 심는 문제는 바로 이 선분 개념을 담고 있다.
도로의 양끝에 나무가 있어야 한다고 했으므로, 오른쪽 끝에 나무 한 그루를 더 심어야 양끝이 막히게 된다.
즉, 나무(성냥개비 머리)의 수= 간격의 개수(성냥개비 몸통)+ 1이다.
아까 성냥개비들을 다시 들여다보자. 그러고 보니 성냥개비 머리로 한 쪽 끝이 비어 있었다. 점으로 시작했지만 점으로 끝나지 않은 것이다. 따라서 이것이 선분이 되려면 끝에 점이 하나 더 있어야 한다.
<도형>에서 선분의 양 끝은 항상 점이어야 한다. 따라서 도로에 나무 심는 문제에서도 양쪽이 막혀있어야 한다는 조건이 있는 것이다. 따라서 도로의 나무 문제는 단순히 나눗셈을 잘 하는 지를 묻는 계산 문제가 아니라 도형의 기본인, ‘선분’에 관한 문제였던 것이다.
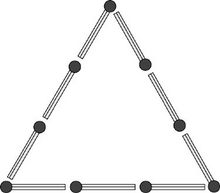
이번엔 삼각형, 사각형, 원과 같은 도형과 연결해서 생각해 보자. 도로에 나무 심는 문제 중에는, 원이나 다각형 모양의 운동장 둘레에 나무를 심는 문제도 있다. 예를 들면, “한 변의 길이가 15m인 삼각형 모양의 운동장 둘레에 5m 간격으로 나무를 심으려고 한다. 나무는 몇 그루 필요한가?” 라는 문제가 있다. 성냥개비 하나의 길이가 5m라고 생각하고 성냥개비를 이어 삼각형 모양의 운동장을 표현해 보자.
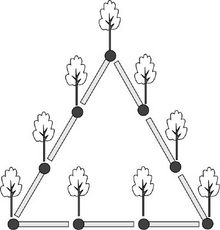
‘직선 도로에 나무 심기’ 문제에서는 도로 길이를 나무 심는 간격으로 나눈 후에 1을 더해야 했지만, 이번엔 1을 더하지 않아도 된다. 왜냐하면, 삼각형은 안과 밖에 구별되는 닫힌 도형이기 때문에 성냥개비를 서로 연결하면 처음과 끝이 서로 다시 만나므로 빈 곳이 없기 때문이다.
성냥개비의 머리에 나무가 있다고 치면, 성냥개비수는 나무의 수와 똑같다.
성냥개비의 수= 나무의 수
성냥개비를 선분으로 생각했기 때문에 이런 설명이 가능했다. 그렇다면 곡선으로 둘러싸인 원은 어떨까? 원에 대해 생각해 보자.
둘레가 100m인 원 모양의 운동장이 있는 데, 운동장 둘레에 5m 간격으로 나무를 심는다고 하자. 이 운동장을 노끈으로 나타내어, 5m마다 나무를 심을 자리를 점으로 표시하자. 100은 5의 20배이므로, 20개의 점이 있게 된다. 점과 점 사이의 ‘끈 부분’과 ‘점’을 짝지어서, 점 앞에서 각각 잘라보자.
점과 선분이 모두 짝이 되므로, 남은 것이 없다. 따라서 원 모양의 운동장 둘레에 나무를 심으면, 간격(선분)의 수와 나무의 수(점)이 똑같다. 이처럼, 언뜻 보았을 때는 나눗셈을 잘 하는 지, 배수와 약수 관계를 잘 아는 지를 묻는 계산문제로 보이는 이런 문제가 실제로는 도형과 깊은 관계가 있다.
강미선/수학 칼럼니스트 upmmt@hanmail.net
광고







기사공유하기