등록 : 2006.07.09 20:20
수정 : 2006.07.10 14:01
수학개념 쏙쏙/ 사각형의 포함관계
누가 “삼각형이 무엇이냐?”고 묻는다면 뭐라고 대답하면 좋을까? 평면 도형, 세 변으로 둘러싸인 도형, 세 각의 합이 180도인 다각형, 기본 도형 중의 하나, 대각선이 없는 도형…. 이 모든 것이 삼각형을 설명한다. 따라서, 삼각형의 어떤 특성-각에 대한 것인지, 대각선에 대한 것인지, 변에 대한 것인지 등-을 알고 싶은지 구체적으로 질문해야 한다.
그렇다면 사각형은 무엇일까?
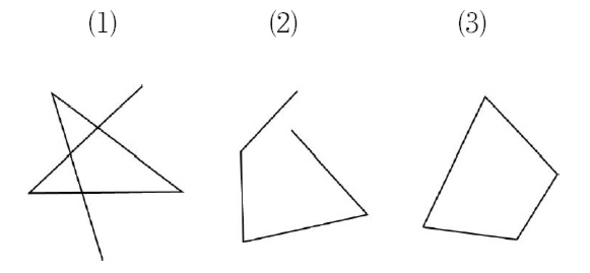
다음은 4개의 선분이 있는 도형이다.
이 중에서 4개의 선분으로 둘러싸인 (3)만 사각형이라고 한다.
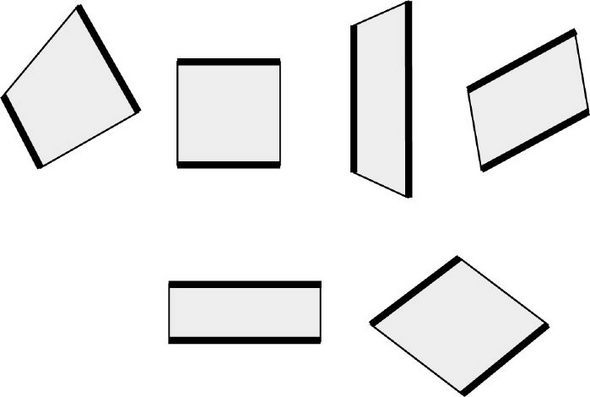
여기 사각형들의 모임이 있다.
이 모임에 있는 사각형을 분류해 보자.
1단계: 두 변의 위치관계로 분류하기
(1) 마주보는 한 쌍의 변이 서로 평행인 사각형들만 모으자.
이런 사각형을 ‘사다리꼴’이라고 한다.
(2) 모임에서 마주보는 두 쌍의 변이 서로 평행인 사각형만 모으자.
이런 사각형을 ‘평행사변형’이라고 한다. 평행사변형은 마주보는 두 쌍의 변이 서로 평행이어야 하므로, 한 쌍이 평행이면 되는 사다리꼴 가운데는 평행사변형이 아닌 사각형도 있었다.
(3) 내각의 크기가 모두 같은 사각형을 모으자.
사각형의 4개의 내각(사각형 안쪽 각)의 합은 360도이므로, 4개의 각의 크기가 모두 같으면 한 각의 크기는 90도가 된다. 90도는 직각이다. 따라서 네 각의 크기가 모두 같은 사각형을 ‘직사각형’이라고 한다. 직각 사각형 중에는 네 변의 길이가 모두 같은 사각형도 있고, 그렇지 않은 사각형도 들어 있다.
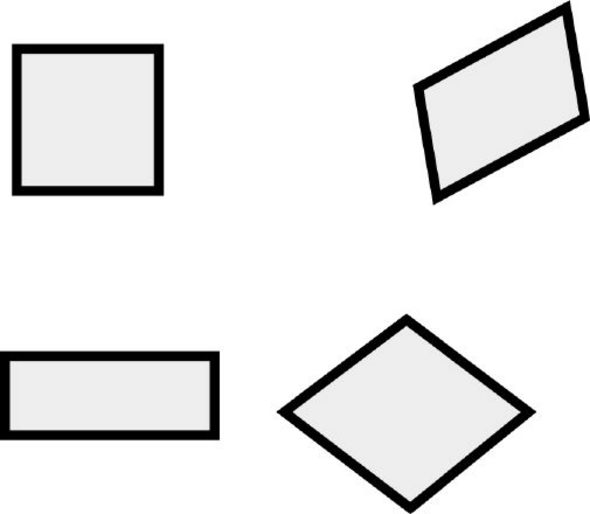
2단계: 변의 길이로 분류하기
(1) 네 변의 길이가 같은 사각형을 모으자
변의 길이가 모두 같은 사각형을 ‘마름모’라고 한다. 마름모는 네 변의 길이가 모두 같지만, 네 각의 크기가 꼭 같을 필요는 없다.
2) 네 각의 크기와 네 변의 길이가 모두 같은 사각형을 모으자.
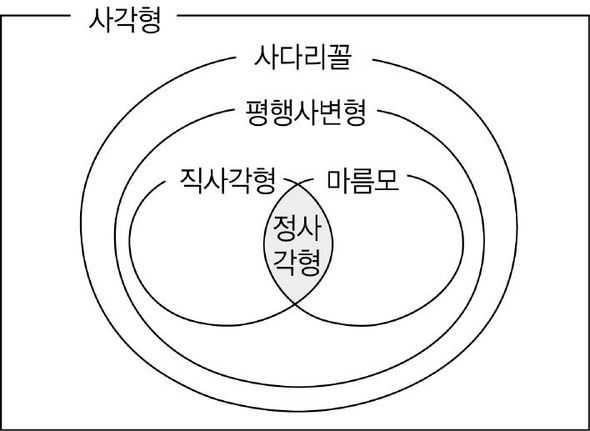
이런 사각형을 ‘정사각형’이라고 한다. 정사각형은, 사다리꼴 모임에도 들어 있었고, 평행사변형 모임에도 들어 있었고, 마름모 모임에도 들어 있었고, 직사각형 모임에도 들어 있었다.
사각형에는 대각선이 2개인데, 정사각형은 대각선의 길이도 서로 같고 수직으로 만난다. 이상에서 알아본 것을 통해 다음 관계를 알 수 있다.
강미선/수학 칼럼니스트
upmmt@hanmail.net
광고












기사공유하기