다툼없는 유산분배 ‘이산수학’에 맡겨주세요

논리로 배우는 수학 /

종중의 땅은 여자에게는 줄 수 없다?

지난 4월28일 대법원은 용인 이씨 사맹공파의 출가 여성 이아무개(73)씨 등 5명이 종중(宗中)을 상대로 낸 종회 회원 확인 청구소송에서 ‘성인 여성에게 종중 구성원의 자격을 인정하지 않는 종래 관습은 법질서에 부합하지 않는다’며 원고 승소판결한 원심을 확정했다. 한편, 법무부는 이달 초 공동상속자의 수와 관계없이 상속 재산의 50%를 배우자의 몫으로 인정해 주는 민법 개정시안을 마련했다.

일반적으로 피상속인의 유언으로 재산의 분배를 결정해 놓으면 원칙적으로 유언에 의하여 승계가 이루어지지만, 유언이 없는 경우에는 자녀들에게 똑같이 분배된다. 다만 현재의 법령으로는 피상속인의 배우자가 있을 때에는 자녀보다 1.5배의 재산을 받는다. 예를 들어 자녀가 1남1녀이고 배우자가 있는 경우에는 배우자에게 재산의 7분의3을 주고, 남은 7분의4를 두 자녀에게 7분의2씩 분배하면 된다. 그러나 배우자가 없을 경우에는 두 자녀에게 각각 2분의1씩 분배하면 된다.

재산을 분배하는 일이 지극히 수학적이라고 하면 믿지 않겠지만, 현행 고등학교 이산수학 교과서 4단원에서 공평한 분배라는 내용으로 재산 분배를 다루고 있다. 예를 들어 보자.

네 자녀를 둔 어떤 가정의 부모가 동시에 사망하였다. 이 가정에 남은 재산은 아파트 한 채와 임야 200평, 그리고 보석 2개와 현금 4천만원이었다. 장례를 치른 뒤 자녀들은 재산을 분배하려고 모였다. 사망한 부모의 유언은 남은 재산을 결코 팔지 말고 네 자녀가 모두 만족하게 나누라는 것뿐이었다. 수학적으로 공평하게 재산을 나누는 방법은 무엇일까? 현행 민법에 따라 유언에 각 자녀의 몫이 주어져 있지 않으므로 모든 자녀는 똑같이 분배하되 유언대로 만족하게 나누는 것이 가장 이상적인 분배가 될 것이다. 이제 모두가 만족하는 재산 분배를 해 보자.

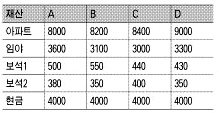
(1) 물건을 팔 때는 그 물건의 값을 가장 비싸게 쳐주는 사람에게 파는 것이 최고의 원칙이다. 그러므로 유산에 대한 분배도 최고 높은 가치를 인정하는 자녀에게 돌아가게 해야 한다. 그러기 위해서는 우선 네 자녀가 모여 각자가 남은 재산의 가치를 적어 내도록 한다. 각 사람이 써낸 재산의 가치 중 최고 높은 가격을 쓴 사람에게 그 재산을 우선 분배하도록 하기 위함이다. 실제로 네 자녀가 써낸 결과가 다음과 같다고 하자.

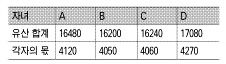
여기에서 각 사람이 생각한 유산의 총액을 구하여 4로 나누면 각 사람이 생각한 자기의 몫을 구할 수 있다. 즉, 각 자녀는 각자의 몫만큼을 유산으로 챙기면 절대로 불만을 가져서는 안 된다.

(2) 유산을 팔 수가 없으므로 물건을 누군가에게 주어야 한다. 지금 분배 원칙, 즉 최고 높은 가치를 인정하는 사람에게 그 물건을 우선 분배하는 원칙에 의하면 아파트는 D에게, 임야는 A에게, 보석 1은 B에게, 보석 2는 C에게 분배된다.

(3) 현금은 똑같이 나눌 수 있으므로 각자에게 1000만원씩 분배한다.

(4) 재산이 모두 분배되었으므로 모두가 만족할 수 있도록 뒷정리를 한다.

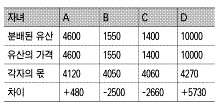
뒷정리를 하기 위하여 먼저 지금까지의 재산 분배 현황을 정리하자. 그리고 최초에 적어낸 각자의 몫과 분배된 재산의 가치의 차를 계산해 보면 다음과 같다.

(5) 위 계산 결과에 따라 그 차액은 각자가 현금으로 처리를 하는 게 좋겠다. 그러므로 A는 480만원, D는 5730만원을 내놓고, 이 중에서 B에게 2500만원, C에게 2660만원을 준다.

(6) 이렇게 되면 항상 돈이 남게 된다. 지금까지 각 사람은 자기가 최초에 받았으면 하고 써낸 분배를 모두 받았으므로 더 이상의 불만이 있어서는 안 된다. 그런데도 돈이 남았다. 그 이유는 뭘까? 그것은 각 재산을 가장 최고 높은 가치를 인정하는 사람에게 주었다는 것은 곧 그 가격에 팔았다는 것과 같은 결과이므로 이와 같은 방법으로 재산을 나누면 항상 돈이 남게 된다. 그러므로 그 남은 돈 1050만원은 4등분하여 각자에게 262만5천원씩 나눠준다.

이렇게 분배하면

(i) ‘재산을 팔지 말라’는 부모의 유언을 지켰다.

(ii) 각 자녀는 최초에 각자가 생각했던 몫보다 각각 262만5천원씩 더 받은 것이므로 모두가 만족할 것이다.

재산 분배가 끝났다. 그것도 아주 공평하고 모두가 만족하는 방법으로 되었다는 것을 인정할 수 있다. 이산수학 교과서에서는 재산 분배뿐만 아니라 케이크를 분배하는 합리적인 방법과 그 과정도 제시되어 있다. 실제로 수학은 바로 이런 분야에서 계속 발전하고 있다. 21세기 네트워크 시대를 살고 있는 우리들을 돕는 수학, 우리에게 진정 필요한 수학은 바로 이산수학이 아닌가 싶다.

최수일/서울 용산고 교사 [e-mail]