수학개념 쏙쏙
지난 글에서 다음 두 가지 상황에 대하여 고민을 시작하였다. 그것은 똑같은 비율을 올렸다가 내리는 경우에 나타나는 현상에 대한 수학적인 해석이다. 똑같은 물건에 대하여 다음 두 가지 경우의 결과는 어떨까?
(i) 처음에 10% 내렸다가 다시 10%를 올린 경우
(ii) 처음에 10%을 올렸다가 다시 10%를 내린 경우
고민은 두 가지였다. 그것은 (i)과 (ii)의 두 결과가 서로 같을 것인가 하는 것과 어느 경우의 가격이 원상으로 복귀되는 것일까 하는 것이었다. 여기서 얻은 결론은 두 결과는 서로 같지만 두 경우 모두 가격이 원상으로 복귀되지 않는다는 것이었다.
둘 다 상식적으로 이해가 가지 않는 부분이다.
물론 위와 같은 상식을 가지고 있는 사람도 있겠지만 예전의 어느 텔레비젼 프로그램의 하나였던 <100명에게 물어봅시다>에서와 같이 100명에게 물었더니 거의 모두가 위와 같은 상식을 가지고 있지 않았다. 그러나 수학을 이용하면 우리의 상식이 잘못되었음을 정확히 설명할 수 있다. 두 결과가 같은 것은 수학에서 두 수의 곱셈에서 곱하는 순서를 바꿔도 결과가 같다는 교환법칙이 성립하기 때문이다. 그리고 가격이 원래보다 작아지는 것은 산술평균과 기하평균의 관계로 설명할 수 있다. .
즉, 10%를 인상하면 원금 S원이 S(1+0.1)이 되고, 여기에서 10%를 인하하면 S(1+0.1)(1-0.1)이 되기 때문에 그 결과는 S×0.99이다. 1%가 감소하는 이유는 고등학교 1학년에서 배우는 절대부등식 중의 하나인 산술평균과 기하평균의 관계 때문이며, 그것은 a=1-0.1, b=1+0.1로 두었을 때, 두 값의 합은 a+b=2이고 부등식 에서 두 수의 곱 ab는 두 수가 같을 때 최대가 되기 때문에 원래의 가격이 가장 크고, 위와 같이 두 번 바뀌면 그 결과는 항상 작아지는 신기한 현상을 설명할 수 있다.
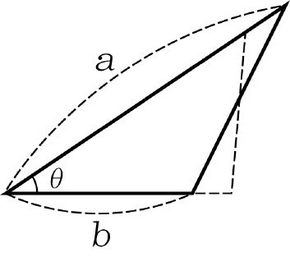
이런 현상은 비단 물가에만 일어날까? 도형 문제로 넘어가 보자. 다음 그림과 같이 삼각형의 한 변의 길이를 10% 늘이고, 다른 한 변의 길이를 10% 줄여서 새로운 삼각형을 만들 때, 삼각형의 넓이는 어떻게 변하겠는가? 물가를 따질 때와 같은 호기심을 가질 수 있다. 넓이는 변하지 않을 것 같다.
아니면 긴 변을 늘일 때는 커지고, 긴 변을 줄일 때는 작아질까? 결론은 어느 경우든 넓이가 1% 감소한다. 계산은 다음과 같다. 처음 삼각형의 넓이를 라 하면
새로운 삼각형의 넓이를 S 라 하면
따라서 넓이는 1% 감소한다. 신기한 일이지만 수학적 사실은 모든 경우에 예외가 있을 수 없다. 그것이 바로 수학의 매력이다.
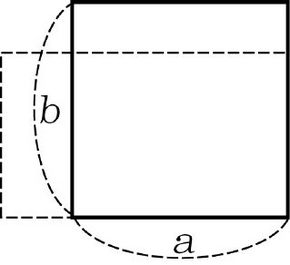
직사각형에서도 이런 일이 벌어질까? 다음 그림의 직사각형의 가로의 길이를 20% 늘이고, 세로의 길이를 20% 줄여서 새로운 직사각형을 만든다. 처음 넓이를 S라 하면 S=ab이고, 새로운 직시각형의 넓이를 S라 하면
따라서 넓이는 4% 감소한다.
거듭되는 얘기가 되지만 왜 변하기만 하면 크기(넓이)가 줄어드는 것일까? 그것은 물가와 마찬가지의 설명으로 하면 산술평균과 기하평균의 관계로밖에 설명할 길이 없다. 물론 두 평균의 관계를 이해하려면 현재 우리나라의 교육과정으로는 적어도 고등학교 1학년 1학기는 지나야 하므로 중학생까지는 그런 것으로 인정할 수밖에 도리가 없다.
이제 중학생도 이해할 수 있는 소재로 이 얘기를 넓혀 보자. 다음 세 실수 의 대소 관계를 조사해 보자..
이와 같은 무리수들은 직접 그 대소 관계를 알 수 없기 때문에 제곱을 하여 비교한다. 각각을 제곱하면
즉, ( )이므로 a>b>c임을 알 수 있다.
이 정도의 가벼운 수를 비교하는 것은 그리 어렵지 않다. 이제 다음과 같이 본격적으로 큰 수를 조사해 보자.
제곱해 볼까? 엄두가 나지 않는다.
그러나 중요한 것은 위의 작은 세 수를 제곱할 때 뭔가 눈치를 챘어야 한다.
a가 가장 큰 이유는 물론 제곱해봐서 알 수도 있지만 제곱하지 않고도 알 수 있다. 그것은 주어진 세 수 a, b, c의 근호 안의 수의 합이 모두 10이라는 공통점이 있어서 제곱의 유리수 부분이 모두 10으로 같아졌고,
무리수 부분은 근호 안이 이들의 곱이기 때문에 산술평균과 기하평균의 관계를 생각할 수 있다.
즉, 합이 일정할 때 곱은 두 수가 같을 때가 최대이고 차이가 벌어질수록 작아짐을 짐작할 수 있다. 바로 이 점에서 큰 수 A, B, C의 제곱을 하지 않고도 근호 안의 두 수의 합이 모두 10,000이므로 그 두 수의 곱의 비교로 대소가 결정할 수 있다는 똑같은 논리에 의해서 가장 큰 수는 A임을 알 수가 있는 것이다.
산술평균과 기하평균의 관계는 변하는 두 수치를 가진 것들을 비교할 때 물가나 도형이나 무리수나 할 것 없이 똑같이 적용되는 수학의 진리임을 깨닫는 계기가 되기를 바란다.
최수일/서울 용산고 교사
choisil@hanmail.net
광고

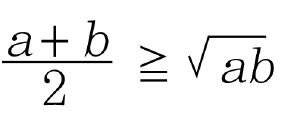
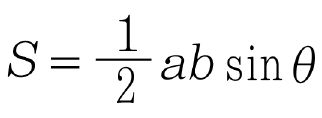
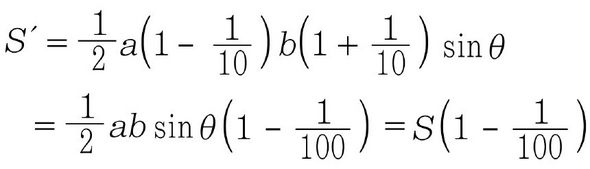
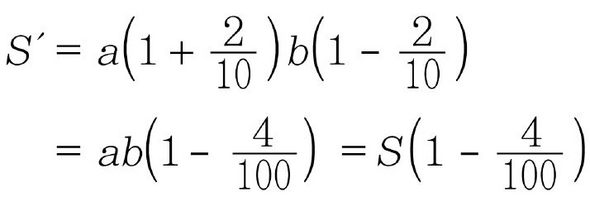
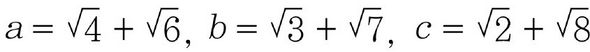
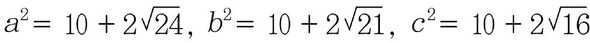
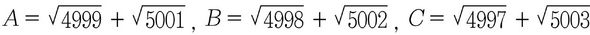

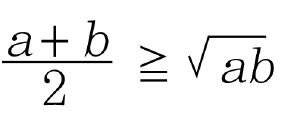

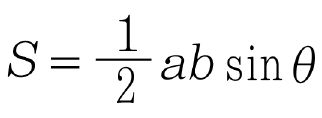
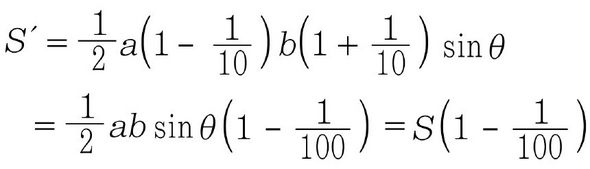

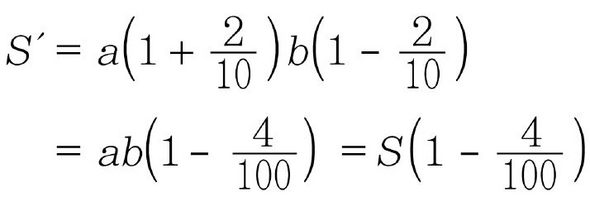
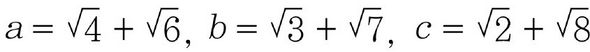
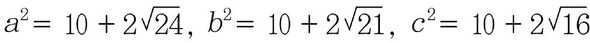
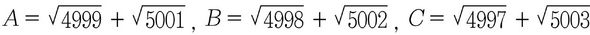
기사공유하기