잃어버린 면적 ‘1‘은 어디로?

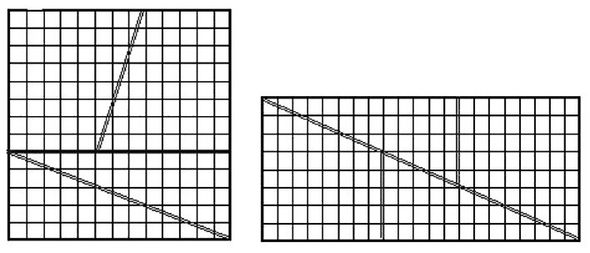
창의력 쑥쑥 퀴즈

자연에 나타나는 다양한 수열 중에서 피보나치 수열(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …) 은 식물의 꽃잎 수, 돌려나기 잎차례, 솔방울의 회전 수 등에도 나타나고 특히 앞, 뒤 수의 비율이 황금비를 보여주기도 한다. 피보나치 수열에서 이웃하는 두 수를 선택하여 그 합을 한 변으로 하는 정사각형을 만든다. 이를 직사각형 모양으로 바꾸게 되면 크기가 꼭 1씩 차이가 나게 된다. 예를 들어 5와 8을 선택하여 한 변을 13으로 하는 정사각형을 만들었다가 그림과 같이 8×21 인 직사각형으로 만들 수 있다. 그러나 이때 정사각형은 면적이 13×13 = 169 이고 직사각형은 8×21 = 168 이 되어 면적에 차이가 나타난다. 21과 34를 선택해도 마찬가지이다. 피보나치 수열의 이웃하는 수에 모두 적용이 되는 문제이다. 정사각형에서 직사각형으로 바뀔 때 잃어버린 면적 ‘1’은 어디로 갔을까?

문미옥/이화여대 와이즈거점센터(wise.or.kr) 연구교수

---

[지난주 정답]

초콜릿 피라미드 상자를 한 층 더 만들 때마다 피라미드 상자에 담을 수 있는 전체 초콜릿 수는 1, 5(=1+4), 14(=5+9), 30(14+16), 55(30+25) …로 늘어나게 되는데 이를 피라미드 수라고 한다. 피라미드 수는 제곱수를 계속 연이어 더하게 되는데 1, 4, 9, 16 …으로 이어지는 제곱수에는 다시 4=1+3, 9=1+3+5, 16=1+3+5+7 …로 1, 3, 5, 7, 9 …의 홀수를 연이어 더한 값이 된다.

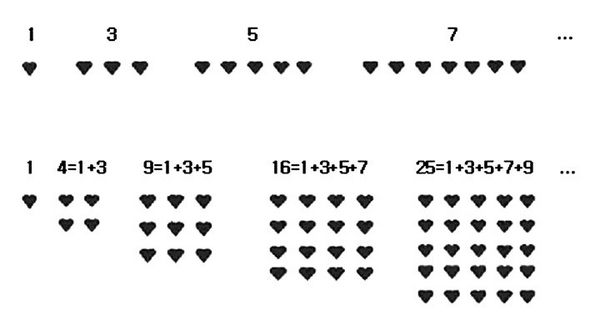그러니까 초콜릿을 140개 담으려면 140=1+4+9+16+25+36+49로 7층으로 된 피라미드 상자를 만들어야 한다. 자연에는 참 다양한 수가 재미있는 특성을 가지고 연결되어 숨어 있다.