등록 : 2006.09.17 18:19
수정 : 2006.09.18 13:50
수학개념 쏙쏙 /
‘회전체’는 초등학교 6학년 2학기와 중학교 1학년 2학기에 배운다. 회전체 단원에서는 두 가지를 배우는데, 회전체의 정의 그리고 회전체의 단면이다. 다루는 내용과 전개방식은 서로 비슷하므로, 6학년 때 배운 것을 중학교에 올라가 다시 배운다고도 볼 수 있다.
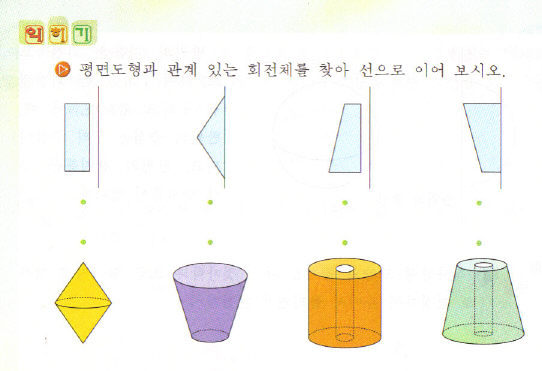
회전체란 무엇이고 회전체의 단면은 어떤 모양일까? 수학은 항상 정의에서 시작하므로, 우선 정의를 살펴보자. 초등학교 6-나 교과서 <입체도형> 단원을 보면 “평면도형을 한 직선을 축으로 하여 1회전해서 얻어지는 입체도형을 회전체라고 한다. 이때 축으로 사용한 직선을 회전축이라고 한다.”고 돼 있다. 이 때 그 직선이 도형에 붙어 있어야 하는 지 아닌지에 관한 언급은 없고, 교사용 지도서에는 “회전축과 평면도형 사이의 공간이 하나의 회전체 모양이 된다는 것을 알게 한다.”는 말이 있다.
중학교 교과서 중에는 “(위와 같이) 직사각형, 직각삼각형의 한 변을 회전축으로 1회전 할 때 생기는 회전체”라고 정의한 경우도 있다. 이렇게 보면 아무 직선이나 회전축이 되는 것은 아니고, 회전축은 평면도형의 일부여야 한다는 생각이 든다. 그렇다면 평면도형과 회전축이 서로 떨어져 있는 입체는 회전체일까, 아닐까?
백과사전 중에는 “평면도형이 동일 평면 안에 있는 직선을 축으로 하여 회전했을 때 생기는 입체”를 회전체라고 하는 경우도 있다(동아대백과사전). 이 때, 회전축이 평면 밖에 있는 경우를 어떻게 해석해야 할 것인지의 여부는 ‘동일 평면’의 정의에 따르는데, 다소 복잡한 개념이다.
이번엔 국어사전을 살펴보자. 대부분의 국어사전에는 회전체의 뜻이 두 가지로 나와 있다. 1. 축을 중심으로 그 둘레를 도는 물체. 2. <수학>평면 도형이 같은 도형 안에 있는 직선을 축으로 하여 회전하여 생기는 입체. 원이 지름을 축으로 하여 회전하면 구(球)가 된다(국립국어원).
1번 뜻으로 본다면, 회전해서 생긴 것은 모두 회전체라고 볼 수 있다. 하지만 2번에 따르면 수학에서의 회전체는 ‘같은 도형 안에 있는 직선을 축으로’ 해야 한다.
단지 회전해서 만들어진 입체들은 모두 회전체라고 볼 수도 있지만, 수학 시간에는 수학적인 정의에 따라야 할 것이다. 수학 6-나 교과서 34쪽의 다음 장면을 보면 초등 수학에서는 회전축이 평면도형과 떨어져 있어도 회전체라고 한다는 것을 알 수 있다.
이번엔 단면에 대해 알아보자. 6-나 교과서에는 원기둥 모양의 무, 원뿔 모양의 당근, 구 모양의 오렌지를 여러 가지 방향으로 잘랐을 때 잘린 면을 살펴보는 활동이 나와 있다. 회전축을 포함하는 평면으로 잘랐을 때, 그 단면은 회전축을 기준으로 서로 대칭인 도형이다. 회전축이 회전체에 붙어있는 경우의 단면은 ‘선대칭 도형’이고, 회전축에 떨어져있는 경우는 ‘선대칭 위치에 있는 도형’이다.
회전체를 회전축에 수직인 평면으로 잘랐을 경우에는
이 된다. 교사용 지도서에서는 “회전축에 수직인 평면으로 자른 단면은 원이라는 것을 발견하도록 한다.”고 쓰여 있다. 또, 7-나 교과서에도 “회전체를 회전축에 수직인 평면으로 자른 단면은 항상 원이다.”라고 되어 있다.
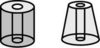
모양의 회전체를 회전축에 수직으로 잘랐을 때 나오는 모양도 원이라고 보아야 할지 혼란스럽기도 하다. 게다가 회전축에 수직인 단면을 묻는 교과서의 활동이나 문제들에는 모두 원기둥, 원뿔, 구와 같이 단면이 하나의 원인 경우만 예로 나와 있다. 회전축이 평면도형과 떨어져서 만들어진 회전체의 단면에 대해서도 살펴보긴 하지만 “어떤 모양이 되는 지 그려보시오.”라고만 되어 있을 뿐 그 모양도 원인지 아닌지 말로써 서술하는 문제는 나와 있지 않다. 그렇다보니 원에 대해 안이 꽉 차야 한다고 생각하는 사람들은 “가운데 구멍이 뚫렸으니 원이 아니다”라는 생각을 할 수도 있다.
원의 정의는 ‘한 점에서 일정한 거리에 있는 점들의 모임’이다. 그러므로 원에 내부는 포함되지 않는다.
은 안쪽 원이나 바깥쪽 원이나 모두 회전축으로부터 같은 거리에 있는 점들로 만들어진, ‘중심은 같지만 반지름이 다른 두 개의 원’으로 보아야 한다. 어쨌거나 회전체를 회전축에 수직인 방향으로 자른 단면은 항상 원이다!
강미선/수학 칼럼니스트
upmmt@hanmail.net
광고

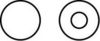



기사공유하기