 |
 |
문미옥/이화여대 와이즈거점센터(wise.or.kr) 연구교수
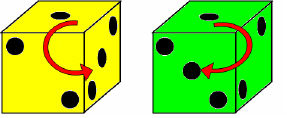
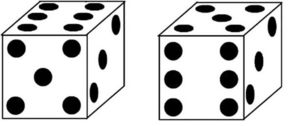
■ 지난주 답 ■ 지구처럼 어마어마하게 큰 공의 허리와 사람 중에서 참 큰 최홍만 허리의 둘레가 늘어났다면 지구는 얼마나 더 커지고 최홍만은 얼마나 살이 더 쪘을까. 원둘레는 2πτ이다. 즉 반지름의 크기를 두 배하여 원주율을 곱하는 것이다. 지구 둘레는 (2π ×지구반지름)미터이고 최홍만의 허리가 동그랗다고 가정하면 그 둘레는 (2π × 최홍만 허리 반지름)인치다. 지구는 둘레를 1인치 늘려 (2π ×지구반지름 + 1 )인치가 되고 최홍만은 1인치 늘여 (2π × 최홍만 허리 반지름 + 1 )인치다. 각각 띠를 고르게 둘렀을 때 늘어난 두께를 계산해보면 지구는 2πτ × (지구반지름+ 1/2π )인치고 최홍만은 2π × (지구반지금 + 1/2π )인치다. 즉 허리둘레가 1인치 늘어날 때 최홍만은 허리가 0.16인치 두꺼워졌고 지구도 딱 그만큼 두꺼워진다. 날씬한 사람이나 뚱뚱한 사람이나 허리가 1인치 늘어났다면 허리의 두께는 똑같이 늘어난 것이다. 그런데 부피로 따지면 또 다르다. 아무래도 뚱뚱한 사람이 더 찐 것이다. 수학이나 과학에는 비율이 많다. 비율의 의미를 잘 안다면 계산 없이도 많은 문제를 의외로 쉽게 해결할 수 있다. 혹시 문제를 풀기 위해 최홍만씨에게 메일을 보내 허리 크기를 물어본 분이 있다면 죄송하게 됐다. 그러나 문제에서 정보를 주지 않으면 그것은 문제를 푸는데 꼭 필요한 정보가 아닐 수 있다는 뜻일 수 있다.
광고


기사공유하기