){kind=link}
){kind=link}
){kind=link}
){kind=link}
){kind=link}
 |
수학개념 쏙쏙 문제를 해결할 때는 대부분 다음과 같은 4단계를 거치게 된다. <폴야(Polya)의 문제해결 4단계> 1단계: 문제를 이해하기 2단계: 어떻게 풀면 좋을지 계획하기 3단계: 계획한 것을 실행하기 4단계: 잘 풀었는지 돌아보기
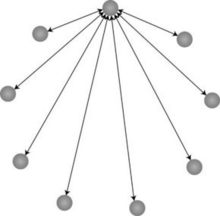
첫 단계인 ‘문제를 이해’한다는 것은 우리가 구해야 하는 것이 무엇인지를 정확히 알아내는 것이고, 그런 뒤 문제 속에 주어진 자료와 조건들을 살펴서 우리가 구하려는 것과 연결해서 풀이에 대한 ‘착상’을 해 계획을 세우는 단계로 들어간다. 구하려고 하는 것이 무엇인지를 아는 것은 매우 중요하다. 예를 들어, 교과서 <5-가>의 8단원에 있는 다음 문제를 생각해 보자. 9명이 서로 다른 사람과 악수를 한다면, 악수를 몇 번 하게 되는가? (악수 문제) 이 문제를 읽고, “여기서 구하고자 하는 것은 악수를 몇 번 하게 되는가이다”’라고 말할 수 있다면, 문제를 잘 이해한 것이다. 다음으로 풀이를 위한 계획을 세워야 한다. 악수를 한 횟수를 구하려면 어떻게 해야 할까? 먼저, 전에 풀었던 것 중에 이와 비슷한 문제가 있었는지 잘 생각해 봐야 한다. 사실 교과서 <4-나> 8단원에 있는 ‘축구 경기에 8팀이 참가하여 각 팀끼리 서로 한번씩 경기를 한다면, 모두 몇 경기를 하게 됩니까?’를 떠올릴 수 있고, 축구 경기 문제와 악수 문제는 같은 문제라는 것을 안다면, 쉽게 해결할 수 있다. 하지만 그것을 꿰뚫어 볼 수 없어서 ‘악수’라는 상황과 ‘축구 경기’라는 상황을 서로 연결해서 생각할 수 없는 학생들이라면, 어떻게 해야 할까? 물론 악수를 실제로 하면서 몇 번이나 악수가 오고갔는지 직접 세어 볼 수도 있다. 저학년이라면 직접 해 보는 것도 필요하다. 아직 악수 경험이 없기 때문에 ‘악수’를 하는 상황 그 자체를 이해하기 힘들기 때문이다. 직접 해보아야만 서로 손을 맞잡은 사람이 두 명일 때 악수를 한 횟수는 한 번만 나온다는 것을 확실히 알게 된다. 그렇다면 5학년은 어떨까? 만약 5학년 아이가 직접 악수를 해 보며 악수의 횟수를 세었다고 하자. 어떻게 답은 알게 될지 모르지만, ‘이런 문제는 왜 푸는 걸까? 악수를 한 횟수를 꼭 구해야 하는 때는 과연 언제일까?’하는 생각이 들 것이다. 악수 문제를 수학 시간에 다루는 이유는, 문제를 해결하는 ‘과정’을 연습하기 위한 것이다. 주어진 문제 상황을 이해하고 어떻게 해결하는 것이 최선인지 생각해서 선택하는 것은, 살아가면서 우리가 매순간 해야 할일이다. 하지만 고학년이 되어서도 규칙을 찾아 쉽게 해결할 생각은 하지 않고 매번 일일이 세려고 한다면, 무의미한 수학 학습이 될 것이다. 4학년까지 배운 ‘문제를 해결하는 여러 가지 방법’은 다음과 같은 여섯 가지 방법이다. 그림 그려 해결하기 표를 만들어 문제를 해결하기 거꾸로 생각하여 문제 해결하기 규칙을 찾아 문제 해결하기 예상하고 확인하여 문제 해결하기 문제를 간단히 하여 해결하기 먼저 ‘그림 그리기’를 해 보자. 그림을 그릴 때 문제에 사람이 나온다고 사람을 그리면 번거롭다(실제로 사람 그림을 그리느라 문제를 풀 시간을 낭비하는 아이들이 있다). 이럴 때는 사람 대신 간단히 점을 그리면 된다. 그럼, 9개의 점은 어떻게 그리는 것이 좋을까? 원 모양으로 그릴 수도 있고 한 줄로 그릴 수도 있다.
 |
|
<그림 1>
|
 |
|
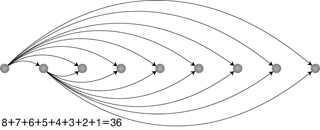
<그림 2>
|
 |
광고
기사공유하기