수학용어, 외우지 말고 이해하라

논리로 배우는 수학 /

2주 전의 글(11월13일치)에서 수학에서 쓰이는 용어는 단순한 약속이 아니라 그런 용어를 사용하게 된 필연적인 이유들이 있다고 주장했다. 그래서 많은 수학 교사들이 수학의 용어의 정의를 영어처럼 막연하게 외우게 하는 것을 볼 수 있지만, 수학 용어의 정의가 그냥 암기만으로 그쳐서는 곤란하며, 학생들이 수학을 공부할 때 이 용어의 정의가 가진 의미를 곰곰 되새겨 보는 것이 수학을 이해하는 하나의 지름길이 될 수 있으며, 수학 용어를 익히는 방법으로 왜 그렇게 정의(定意) 했을까를 고민해 보라고 주장했다. 고민하는 방법 중 하나를 소개하면, 반대되는 경우를 생각함으로써 그렇게 정할 수밖에 없는 필연성을 추측하는 것이다.

다시 ‘집합’ 얘기로 시작을 하자. 중학교에 들어가자마자 첫 수학 시간에 배우는 용어는 ‘집합’이며, 그 뜻은 ‘어떤 기준에 의하여 그 대상을 분명히 알 수 있는 것들의 모임’이라고 돼 있다. 왜 집합을 그렇게 정의했을까? 기준이 없다면 어떤 일이 벌어질까? 대상을 분명히 알 수 없다면 어떻게 될 것인가? 이런 고민은 집합의 정의를 되씹어 보는 것으로 충분히 가능하다. 기준이 없다거나 그 대상이 분명하지 않다면 똑같은 집합을 보고도 각자가 정하는 그 원소나 한계가 다를 것이고, 그 다음부터는 의사 소통이 불가능하게 된다.

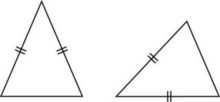
중학교 2학년 2학기에 가면 이등변삼각형의 성질을 배운다. 증명을 배우면서 처음 제대로 된 증명의 시작이 이등변삼각형이고, 그것은 이등변삼각형의 두 밑각의 크기가 같다는 것을 증명하는 것이다. 나는 요즘 우리 학교 인근의 중학생들 몇 명을 모아 방과 뒤에 기하 수업을 하고 있다. 수업 시간에 이등변삼각형을 공부하게 되었는데, 일부러 이등변삼각형의 그림을 돌려서 그렸다. 그것은 밑각이라는 용어의 정의를 학생들이 정확히 모르고 있어서 확실하게 해주려는 의도에서였다.

밑각이 뭐냐고 물었다. “밑에 있는 각이요!” “그래? 그러면 오른쪽 삼각형은 이등변삼각형 맞지? 그럼 이 삼각형의 밑에 있는 두 각의 크기가 같겠네?” “…” 답이 없다. 왜냐하면 밑각에 대한 정의가 틀렸기 때문이다. 이처럼 수학의 용어는 그 정의가 정확하지 않으면 전혀 대화가 되지 않을뿐더러 문제를 해결할 수도 없다.

삼각형의 정의를 보자. 아마도 초등학교 1학년에서 ‘세모 모양’이라고 정의된 삼각형은 초등학교 2학년에서 선분을 정의하면서 ‘3개의 선분으로 둘러싸인 도형’으로 정의가 된다. 삼각형에서 선분이라는 것은 곧 변을 의미하는데, 왜 삼변형이라고 하지 않고 삼각형이라고 했을까? 혹은 삼각형의 정의를 ‘세 개의 각으로 이루어진 도형’으로 정의하면 어떨까 등의 의문을 가져야 한다. 그것은 삼각형이라고 한 것은 다각형(多角形)이라는 용어에서 앞의 ‘다(多)’라는 말 대신 변의 개수를 넣어서 ‘삼각형’, ‘사각형’, ‘오각형’, … 등으로 부르기 때문이라고 생각할 수 있겠다. 그리고 삼각형의 정의를 문자 그대로 해석해서 ‘세 개의 각으로 이루어진 도형’으로 정의한다면 삼각형이 하나로 결정되지 않기 때문이다. 이런 면에서 수학에서 정의를 한다는 것은 유일하다는 전제가 깔려 있다는 것을 알 수 있다. 유일해야만 하는 것은 지구인 모두가 그런 용어를 사용했을 때 모두가 똑같은 대상을 가지고 얘기해야만 의사 소통할 수 있기 때문이다. 그래서 수학의 정의는 유일하도록 만들어야 하는 특성을 가지고 있다.

‘유일성’을 생각하니 떠오르는 것은 소수(素數)의 정의다. 소수는 1과 자기 자신 이외의 약수를 갖지 않음을 알고 있을 것이다. 중학교 1학년에서 처음 배우게 되는 소수를 정확히 정의하면 ‘1보다 큰 자연수 중에서 1과 자기 자신 이외의 약수를 갖지 않는 수’라고 되어 있다. 그러면 1은 소수에서 제외됨을 알 수 있다. 왜 그랬을까? 그것은 ‘소인수분해’를 정의하기 위함이다. 즉, 소인수분해가 유일해야 하는 성질을 생각한 것이다. 12를 소인수분해하면 12=3²×3인데, 만일 1도 소수로 치면 12=2²×3=1×2²×3=1²×2²×3=1³×2²×3=…과 같이 무수히 많은 소인수분해가 가능하게 돼 유일성을 잃어버린다. 그래서 소수에서 1을 제외했다는 것을 이해하면 소수에 대한 상당 부분 이해를 하는 거나 마찬가지다.

수학에서는 또 정의하는 것이 해당 학년의 다른 수학 내용과 일치해야 하는 관계로 똑같은 용어가 상급 학년으로 올라가면 그 뜻이 변하는 것이 있는데, 불행히도 교과서가 그런 부분을 일일이 알려주고 있지 않아서 어렸을 때의 상식을 고등학교나 대학교까지 유지하려는 모습을 종종 볼 수 있다. 그런 것 중에 약수와 배수, 짝수와 홀수가 있다. 이것들을 처음 배우는 때는 초등학교 5학년이다. 초등학교 5학년 때는 음수를 배우지 않았으므로 자연수의 범위에서 약수와 배수를 정의한다. 그리고 중학교 1학년 초기에 다시 나오게 되는데 이때까지도 음수를 배우지 않은 상태이므로 자연수의 범위에서만 생각하게 된다. 그런데 고등학교 1학년에 가면 또 약수와 배수를 배우게 되는데, 이때는 수에 대한 것이 아니라 다항식의 약수와 배수를 배우므로 역시 음수에서 약수와 배수를 정의하지는 않고 있다. 그러나 실제로 다음과 같은 문제를 보라.

문제 : 72의 양의 약수의 개수를 구하여라.

이것은 이미 문구에서 알 수 있듯이 음의 약수가 있다는 얘기이다.

또한 고등학교 1학년에서 ｘ³+2ｘ²-5ｘ-6과 같은 고차식을 인수분해할 때는 인수정리를 이용해야 하며, 상수항(-6)의 약수를 대입하여 근을 찾게 되는데, 이때에도 음의 약수를 대입해야 한다. 즉, -6의 약수인 ±1, ±2, ±3, ±6을 대입해야 한다.

정리하자면, 수학에서 나오는 용어의 정의는 그냥 약속이므로 아무 생각없이 외우는 것으로 끝나는 것이 아니라 곰곰 그 이유를 생각해 보아야 한다. 그래야만 그 용어에 관한 이해를 더 깊이 할 수 있을 뿐만 아니라 그 용어가 나오는 문제를 해결할 때에도 큰 도움을 받을 수 있다는 것을 명심하자.

최수일/서울 용산고 교사 [e-mail]