둘레가 같으면 넓이도 같다?

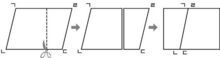
수학개념 쏙쏙 / “기다란 빨대를 잘라서 직사각형을 만들었어요. 이 직사각형을 눕히면 넓이는 커질까. 작아질까, 아니면 똑같을까요?”

선생님이 질문하자 아이들이 손을 번쩍번쩍 들었다.

“달라요!” “똑같아요!”

선생님은 동시에 대답한 호철이와 승규에게 왜 그렇게 생각하는지 그 이유를 설명해 보라고 하셨다.

호철이는 “다르게 생겼으니까요”라고 대답했고, 승규는 “둘레하고 넓이는 관련이 있습니다. 모양이 달라져도 길이는 변함이 없으니까 당연히 넓이도 똑같게 됩니다”라고 했다. 두 아이의 대답을 들은 선생님은 고개를 갸우뚱거렸다.

“다른 의견 있는 사람?”

그러자 이번에는 민주와 형욱이가 동시에 손을 들었다.

민주는, “넓이는 똑같습니다. 왜냐하면 교과서에서 배울 때 평행사변형을 직사각형으로 바꾸면 된다고 배웠기 때문입니다”라고 했다. 선생님은 형욱이도 그렇게 생각하느냐고 물었다. 형욱이는 “직사각형을 눕히면 둘레는 변함이 없습니다. 밑변도 똑같습니다. 하지만 높이가 낮아집니다. 그러니까 넓이는 작아집니다”라고 답했다.

4명 가운데 맞는 사람이 있을까?

형욱이가 맞았다. 직사각형의 넓이는 ‘가로×세로’고, 평행사변형의 넓이는 ‘밑변×높이’다. 두 번째 도형의 밑변은 처음 도형과 같다. 그렇다면 높이는? 높이는 ‘평행한 두 밑변 사이의 거리’인데, 도형을 눕히는 바람에 두 밑변 사이의 거리가 더 가까워졌다. 따라서 넓이도 작아진다.

형욱이는 둘레와 넓이에 관한 개념이 잘 잡혀 있는 학생인 셈인데, 나머지 세 명처럼 잘못 생각하고 있는 학생들도 꽤 많다. 호철이는 모양이 다르면 무조건 넓이도 달라진다고 생각했다. 두 도형의 넓이는 모양으로 구별하는 것이 아니라 계산을 해서 구한다. 모양은 다르지만 넓이가 같은 도형도 있다. 예를 들어 가로가 3cm이고 세로가 4cm인 직사각형과 가로가 2cm이고 세로가 6cm인 직사각형은 모양은 다르지만 넓이는 같다.

민주와 같이 생각하는 학생들도 많다. 그 이유는 교과서(5-가, 98쪽)에서 평행사변형의 넓이를 구할 때 평행사변형을 잘라서 직사각형 모양으로 변형해서 설명하고 있기 때문이다.

이러한 변형은 밑변과 높이에는 변함이 없도록 했기 때문에 넓이가 달라지지 않은 것이지, 만약 빨대로 만든 평행사변형을 세워서 직사각형을 만들었다면 높이가 늘어서 넓이도 달라졌을 것이다.

또 교과서에는 다음과 같은 공식이 제시돼 있다.

이 식만 보면, 모든 평행사변형의 넓이가 직사각형의 넓이와 같다는 오해를 할 수 있을 것 같다. 하지만 어디까지나, 밑면과 높이가 같을 때에 한해서 평행사변형과 직사각형의 넓이가 같다.

또 승규처럼 둘레가 같으면 넓이도 같을 것이라고 생각하는 학생들도 있다. 그러나 둘레와 넓이는 서로 관련이 없다! 평면도형의 둘레의 길이는 평면도형을 이루는 변들의 합이고, 넓이는 그 도형을 덮는 데 사용된 단위 정사각형(한 변의 길이가 1인 정사각형)의 개수다.

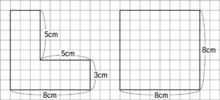
(가)(앞그림) (나)

두 두형의 둘레의 길이를 구하면 똑같다. 그렇다면 넓이도 같을까? 언뜻 보기에도 도형 (나)의 넓이가 도형 (가)보다 크다. 실제로 구해보면 도형 (가)에는 1㎠가 39개 있으므로 넓이는 39㎠이고, 도형 (나)는 64㎠이다. 결국 둘레는 같지만 넓이는 달랐다. 둘레와 넓이의 정확한 개념과, 둘레에 따라 넓이가 달라지는 것이 아니라는 것을 잘 알아두자.

강미선/<행복한 수학 초등학교> 저자 [e-mail]