등록 : 2006.12.24 20:27
수정 : 2006.12.24 20:30
창의력 쑥쑥 퀴즈 /
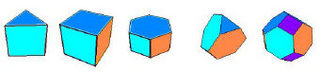
다각형으로 평면을 채우는 문제에서 한 단계 더 나아가 다면체로 겹치지 않게 빈틈없이 공간을 채우려면 쉽게 생각해 볼 수 있는 것이 평면을 채우는 다각형을 그림의 앞 세 도형처럼 기둥으로 만들어 채워나가는 것이다. 플라톤의 다면체 가운데 정육면체가 유일하게 공간을 그러한 방식으로 채울 수 있다. 아리스토텔레스는 정사면체로 공간을 겹치지 않게 빈틈없이 채울 수 있다고 했지만 불가능하다는 것이 알려졌다.
1914년에 푀플이 사면체와 사면체의 끝을 자른 꼴(그림 왼쪽에서 네 번째)을 조합하면 공간을 채울 수 있다고 했다. 8면체와 8면체의 끝을 자른 꼴(그림의 맨 오른쪽), 그리고 정육면체를 잘 조합하면 그 조합의 반복으로만 공간을 겹치지 않게 빈틈없이 채울 수 있다. 어떻게 조합해야 할까?
문미옥/이화여대 와이즈거점센터(wise.or.kr) 연구교수
■ 지난주 정답 ■
겹치지 않게 육각형을 깔아 평면을 빈틈없이 채울 수 있는 경우는 1)마주 보는 변 두 개만 길이가 같은 경우 2)마주 보는 변 한 쌍의 길이가 같고 그에 이웃하는 변 두 개가 길이가 같은 경우 3)마지막으로 이웃하는 변끼리 각각 길이가 같은 경우다. 그 외에는 불가능하다. 그리고 7각형 이상의 도형으로는 어떠한 경우에도 한 가지 도형으로만 평면을 꽉 채울 수 없다. 그런데 수학자와 과학자의 차이를 보여주는 재미있는 발견이 있다. ‘겹침 없음’이라는 조건을 과감하게 버리면 기존의 단위격자 배열로는 기술할 수 없는 새로운 부류의 준결정체 구조 모델을 만들 수 있다. 스타인하르트 박사와 정형채 박사는 1996년 10각형 모양을 기본 구조로 하는 준결정체 구조 모델을 제시했다.
광고
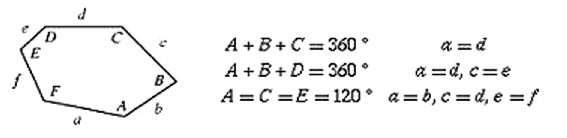


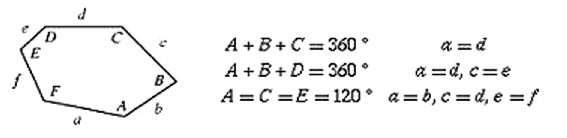

기사공유하기