‘자릿값’을 알자

수학개념 쏙쏙

수학개념 쏙쏙 /

지금 우리는 10을 하나의 단위로 하는 십진법을 사용하고 있다. 십진법에 사용된 수가 10개라는 것은 잘 알고 있을 것이다. 십진법은 1부터 10까지가 아니라 0부터 9까지의 10개의 수를 사용한다.

‘흠! 1부터 10까지든, 0부터 9까지든, 그게 뭐 그리 중요하지?’라고 생각하는 사람들을 위해, 좀더 자세히 알아보자.

0부터 9까지는 각기 다른 모양의 숫자다. 그런데 9 다음 수인 ‘10’은 기존의 1과 0을 사용했다. 숫자들을 다시 반복해서 사용하고 있는 것이다. 이렇게 기존의 숫자들을 차례로 사용하면 10부터 99까지 나타낼 수 있다. 물론 99 다음에 새로운 숫자를 또 만들어 쓸 수도 있다. 하지만 인류의 선조들은 자리에 따라 가치를 다르게 매기는 방법(위치적 기수법)을 선택했다. 이에 따라 99 다음 수는 100이 됐다.

1부터 9까지는 한 자리 수이지만 십진법의 단위인 10이 되면 그 때부터 한 자리 더 늘어서 두 자리 수가 된다. 또 10이 10만큼 모이면 세 자리 수인 100이 된다. 숫자끼리 나란히 붙어 있지만 왼쪽 자리의 가치가 오른쪽 자리의 10배다. 초등학교 6년 동안 우리는 자연스럽게 이런 성질들을 익히게 된다.

중학교에 올라가면 십진법 외에 이진법도 배운다. 십진법만 잘 알면 이진법도 쉽다는 말은 정말일까?

켜짐(1), 꺼짐(0), 단 두 가지 기호로 여러 가지 신호를 보낼 수 있는 컴퓨터에는 이진법이 사용된다. 이진법은 숫자를 2개(1과 2가 아니라, 0과 1)만 사용하는 진법이다. 이진법에서 0 다음 수는 1이다. 1까지 쓰고 보니 이진법에서 사용할 수 있는 숫자는 벌써 다 썼다. 이진법에서는 1 다음은 2가 아니라 10(2)(“이진법의 수, 일영”이라고 읽는다)이다. 2는 이진법의 단위이므로 두 자리 수가 된 것이다. 이것은 십진법에서 9 다음 수가 10이 된 것과 마찬가지 원리다. 삼진법에는 3이라는 숫자 없이 0, 1, 2 세 개의 숫자만 사용한다. 따라서 0(3), 1(3), 2(3) 다음은 10(3)이다. 5진법에서는 4(5)의 다음 수는 10(5)이고, 9진법에서는 8(9) 다음 수는 10(9)이다. 그 진법의 단위가 되는 수의 차례가 되면 한 자리가 올라간다. 이것은 모든 진법에서 공통이다.

수에는 자연수뿐 아니라 소수도 있다. 소수는 분수를 십진법에 맞게 나타내기 위해 만들어진 수이다. 따라서 소수에도 자릿값이 있다.
111.111을 덧셈으로 전개하면,

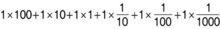123.4567을 전개하면,

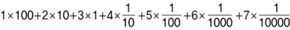자연수도 소수와 마찬가지로 오른쪽으로 갈수록 자릿값이 작아지는데 그 값은 왼쪽 자리의 10분의 1이다. 소수점을 기준으로 생각하면, 소수점 왼쪽으로 갈수록 자릿값은 ‘1, 10, 100….’이지만, 오른쪽으로 갈수록 ‘1/10, 1/100, 1/1000…’이다.

이번엔 이진법 소수에 대해 생각해 보자. 십진법과 마찬가지 원리로 이진법에서는 소수점을 기준으로 왼쪽으로 갈수록 자릿값은 ‘1, 2, 4…’이고, 오른쪽으로 갈수록 ‘1/2, 1/4, 1/8…’이다.
따라서 111.111(2)을 십진법으로 전개하면,

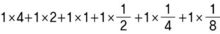이번엔 1010.10101(2)을 전개해 보자.

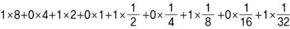지금까지 알아본 바와 같이 ‘자릿값’이라는 아이디어는 자연수뿐 아니라 소수에도 쓰이고, 십진법뿐 아니라 이진법 등 다른 여러 진법에도 쓰인다.

이것은 개념을 학습하면 하나를 배워 열을 깨닫는 효과가 있을 수 있음을 확인시켜 준다. ‘진법’을 초등학교 때는 배우지 않았는데 중학교에 올라가 처음으로 배운다고 생각하는 학생들이 많다. 또 소수 자릿값을 배운 적이 없다고 생각하는 학생들도 있다.

하지만 그동안 미처 깨닫지 못했을뿐, 진법의 기본 개념과 원리는 초등학교 때 이미 배워 왔고, 배우고 있다. 초등학교 때 자연수와 소수의 자릿값에 대해 잘 배워두면, 중학교 1학년 때 배우게 되는 ‘진법’ 단원도 어렵지 않게 배울 수 있다. 강미선/<행복한 수학 초등학교> 저자 [e-mail]