그림·물건으로 문제풀이 해보자

수학개념 쏙쏙

초등 저학년 어린이들에게 수학 문제를 설명할 때는 실제로 행동을 하며 상황을 재연하거나 그림 그리기, 또는 구체물을 활용하는 것이 좋다는 것은 잘 알려진 사실이다. 아직 어리기 때문에 눈으로 보고 손으로 만지는 경험이 중요하기 때문이다. 하지만 많은 부모들은 “너무 유치하지 않을까? 매번 그렇게 설명해야만 한다면 시험 때는 어떻게 하지?”라고 한다. 어엿한 초등학생이라도 상징적 표현 그대로를 이해하기는 무리가 있는 어린 아이들인데 이를 이해하지 못하는 것이다. 어른들은 그동안 알게 모르게 쌓여진 경험으로 숙련돼 있다. 지금 당장 수학 책으로 공부를 하고 있지 않다 뿐이지, 매일 뉴스를 보고 기자가 설명하는 각종 표와 그래프를 보며 지내고 있다. 수학은 이미 수학책을 벗어나 일상 속에 스며들어 있는 것이다.

아이들은 어떨까. 어른들만큼 세상을 경험하지 못해서 책이나 문제집 속에 들어있는 수학을 배우는 중이기 때문에 아주 미세한 부분에서 어른의 생각을 따라가지 못하는 데, 어른들이 눈치 채지 못하고 있는 건 아닐까. 어떤 아이가 다음과 같은 문제를 풀려고 한다.

‘100원짜리와 50원짜리로 500원이 되는 경우를 알아보시오’(2-나)

요즘에는 7살 아이들이 이런 문제를 풀기도 하는데, 정규 교육과정에서는 2학년 문제이다. 이 아이가 유치원생이든, 2학년 아이든 간에, 지금이 이 문제를 해결하는 처음 순간이라고 하자. 아이와 함께 이 문제를 읽은 부모는 ‘동전을 가져와서 설명할까?’ 하는 생각이 스치지만, ‘2학년씩이나 되었는데….’ 혹은 ‘그래도 수학을 잘하는 편인데…’ 싶어서 그냥 종이 위에 연필로 써가며 문제를 설명하기로 한다.

“자, 어떻게 풀면 좋을까?”

아이 표정을 살피지만 낯선 문제를 본 아이는 그저 멀뚱거리기만 한다.

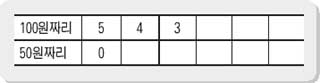
몇 초간 기다리고 나서, “음, 이런 문제는 표를 만들면 된단다.” 하고는 부모가 먼저 다음과 같은 표를 그린다.(이 표는 교과서에 있다)

“문제에서 500원을 만들라고 했잖아. 그러니까 100원짜리 5개가 있으면 50원짜리는 없어도 되지? 그래서 이렇게 표에 5와 0을 쓰는 거야. 자, 이번엔 그 다음 칸을 보자. 만약 100원짜리가 4개라면 50원짜리는 몇 개가 필요하지?”

아이는 고개를 끄덕이며 표에 숫자를 쓰고, 이런 식으로 표를 완성한다. 아이는 이 문제를 확실히 이해했을까?

다음 날 비슷한 문제를 보게 되었다.

‘50원짜리와 10원짜리로 300원이 되는 경우를 알아보시오’

“이 문제 어떻게 푸는지 알지? 어저께 똑같은 문제 풀었잖아. 이번엔 네가 먼저 시작해 봐.”

하지만 아이는 처음 본다는 듯 가만히 있다가, “어떻게 해야 해요?”라고 묻는다.

‘그새 까먹다니!!!’ 부모는 기가 막힌다.

“표를 만들어야지. 전에 풀 때 그렇게 했었잖아.”

눈치를 보다가 대충 표를 만든 아이가 묻는다.

“표에 뭐라고 써요?”

“세로로 50원, 10원, 그리고 가로로는 일단 빈 칸을 여러 개 그려놓고 채워야지.”

일일이 시키면서 억장이 무너진다. ‘왜 얘는 어제 풀었던 문제를 기억하지 못하는 것일까?’ 싶다.

이 문제를 처음 풀던 날, 부모와 아이는 문제를 같이 읽었다. 하지만 부모가 재빨리 상황을 파악한 만큼 아이는 그렇게 확실히 이해할 수는 없다는 것을 미처 몰랐다. 수학을 열심히 공부했던 사람이든 아니든 많은 어른들에게 이런 ‘동전 문제’는 익숙하기 때문에 문제를 읽음과 동시에 문제를 파악할 수 있었다.

분명, 10원짜리 10개는 100원짜리 1개와 모습이 다르다. 하지만 ‘값’은 같다. 이것은 마치 한 개 1000원짜리 사과 5개와 한 개 5000원짜리 배 1개는 분명 서로 다르지만 값이 같은 것과 비슷하다. 하지만 항상 100원이 10원짜리 10개와 같은 것은 아니다. 이용료가 100원인데, 10원짜리 10개는 받지 않고 100원짜리 동전 1개만 받는 보관함도 있다.

다시 처음 문제로 돌아가자. 문제를 풀 수 있는 여러 가지 힌트들을 알려주면 그 아이는 표에 맞는 정답을 쓸 수는 있을 것이다. 하지만 왜 이런 표를 그려야 답을 잘 알게 되는 지, 왜 표를 그릴 때 100원짜리가 5개인 경우부터 시작되는지를 납득하지 못한 채 지나간다면, 다음에 비슷한 문제를 만났을 때 풀이법을 기억해 내지 못할 수 있다. 그러다 몇 번 헤매고 나서야 “이런 유형은 표를 그린다.”고 거의 외우는 경우도 있다.

만약, 이 문제를 풀 때 동전을 직접 가지고 풀면 어떨까. 100원짜리와 50원짜리 동전을 잔뜩 쌓아놓고 500원 만들기를 하는 것이다. 실제로 이렇게 해 보면, 아이들은 처음엔 표를 만들지 못한다. 그런 생각을 아직 못하는 것이다. 자기 나름의 방식대로 여기저기 아무렇게나 쓰다 보니 빼놓는 경우도 생긴다. 답을 다 구했다는 아이에게, “너희가 구한 게 한 가지도 빼놓지 않았다는 게 확실하니?” 하고 물으면, ‘한 가지도 빼놓지 않았다는 것을 어떻게 하면 확신하게 될까?’를 고민하게 된다. 그러다가 나무 가지 모양을 그려 보거나 표(목록)를 생각해 낸다. 이런 과정을 통해, 되는 대로 쓰기 보다는 ‘표 만들기’가 가장 확실한 방법이라는 것을 알게 된다.

‘표’는 우리의 생각을 정리하는 추상적인 수단이다. 처음부터 표를 가르치기 보다는 구체물이나 반구체물로 직접 경험을 하게 도와준다면, 추상적인 표현인 표의 의미도 확실히 이해하고 목적에 맞게 잘 사용할 수 있게 될 것이다. ?

강미선/<행복한 수학 초등학교> 저자 [e-mail]