꼭지점만 점이라고?

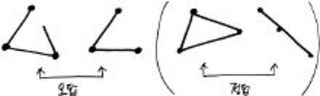수학개념 쏙쏙-꼭지점만 점이라고? 선분 자체가 무수한 점인걸

수학개념 쏙쏙

　“서로 다른 세 점을 곧은 직선으로 잇는다면 어떤 모양이 되는지 알아 보시오.”

이 문제의 답은　‘삼각형’과　‘선분’이다. 하지만 다른 모양을　그리는 아이들도 있다. 어떤 아이는 시작하는 부분과 선분들이 서로 만나는 부분에는 점을 표시하지만 선분의 한 끝에는 점을 표시하지 않은　그림을　그린다. 왜　그렇게　그렸냐고 물으니,　“점은 세 개여야 하니까요”라고 한다. 이 도형에는 점이 세 개 뿐일까?

모든 선의 끝은 점이다. 또한 선은 점들의 집합이므로 이 도형에는 무한히 많은 점들이 있다.　그런데 왜 이 도형의 점이 세 개뿐이라고 생각하는 것일까? 우리가　삼각형을　그릴 때를 떠올려 보자. 자와 컴퍼스를 가지고 삼각형을 작도할 때는 주어진 조건에　따라 점의 위치를 정한 다음, 선으로 연결한다. 하지만 작도를 배울 때를 빼고는 점을 먼저 찍은 일은 별로 없다. 대부분 직선을　그리다가　중간에　적당히 두 번 꺾어서 처음에　시작했던 지점에서 만나도록 마무리를 한다.　그러고는 선이 꺾인 위치에　점(꼭지점)을 표시한다. 이 과정을 따라하다가　자연스럽게 점은 곧 꼭지점이고, 꼭지점들만이 점이 되는 것이라고 생각하게 됐을 수도 있다.

이런 오개념을 바로잡아 주려면,　“세 점을 이어 삼각형을 만드는 것과 삼각형 위의 세 점을 찾는 것은 서로 별개다”라는 것을 강조하는 것이 좋다. 일직선 위에　있지 않은 세 점을 이으면 삼각형이 된다. 하지만 삼각형 위에서 찾을 수 있는 서로 다른 세 점은 무수히 많다. 선분은 점들로 이루어져 있기 때문이다.　교과서의 점판　그림이나 점판　교구를 사용하면 이런 내용을 설명하기가　수월하다. 점판에는 많은 점들이 있으므로, 되도록 커다란 도형을 만들면 선 위에　점들이 놓이게 된다. 이것을 직접 눈으로 확인하면서　“꼭지점만 점이 아니다”라는 것을 강조하자.　　강미선/<초등수학 놀이북> 저자 [e-mail]